Euler's theorem states that given any polyhedron topologically equivalent to a sphere, the number of faces plus the number of vertices will be 2 more than the number of edges.

F + V - 2 = E

For example, a cube has 6 faces, 8 vertices, and 12 edges.

A dodecahedron has 12 faces, 20 vertices, and 30 edges.

Etc.

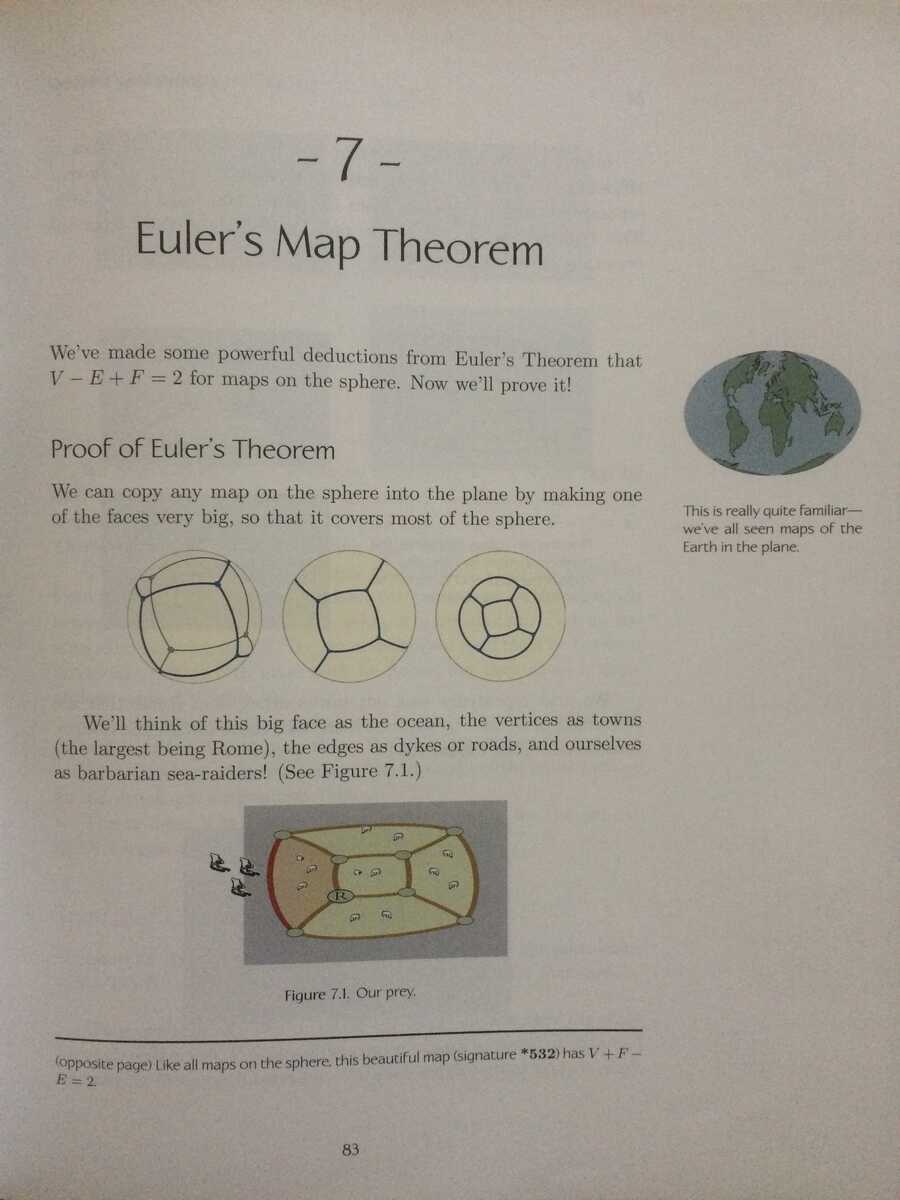
We take our polyhedron (let's say a cube) and declare one of the faces to be the "ocean".

Then we unfold our polyhedron so that we have one large "land mass" surrounded by ocean.

This is analogous to how we can take a globe and unfold it to make a flat map.

Now, we will pretend we are barbarian sea raiders invading this land mass!!

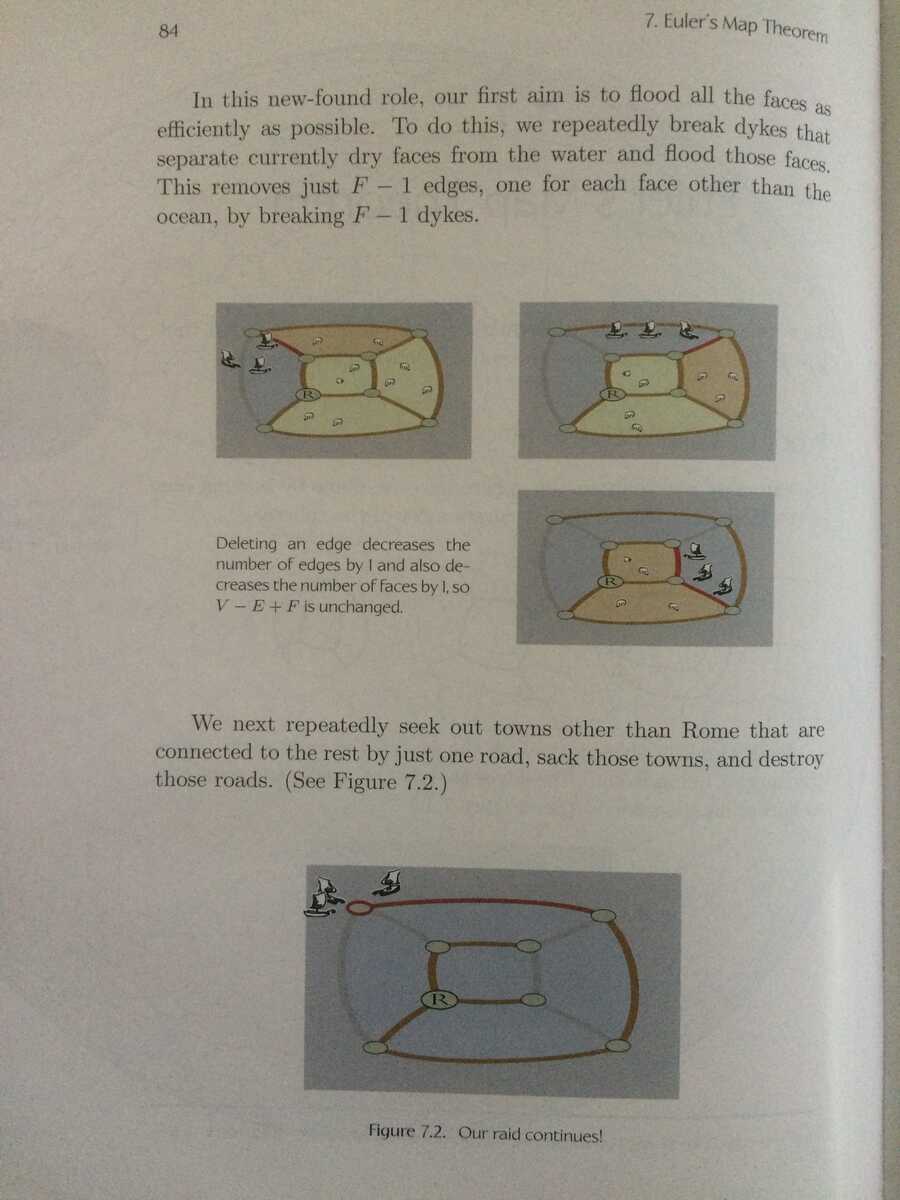
The edges are dykes which we can break to flood the faces.

Our first step in conquering the world is to repeatedly break dykes that separate currently dry faces from the water and flood those faces. Each time we destroy one face and one edge until we've flooded all the faces.

Now, the green vertices are towns. We can pillage any town that is connected to the rest by only one edge. Each time we destroy one town and one edge.

Eventually there's only one town left, which we pillage.

Here's a video of the whole process:

Hooray! We've pillaged everything!

Now, if you were counting along, we started by flooding one face (when we declared it the ocean). Then we destroyed one face and one edge each time. Then we destroyed one vertex and one edge each time. Finally we destroyed the last vertex.

Thus the number of edges is equal to the number of faces (minus 1, the initial ocean) plus the number of vertices (minus 1, the last town).

E = (F - 1) + (V - 1)

Therefore,

F + V - 2 = E

That this works is easier to see if you play the game. The hard part for me to convince myself was that the whole thing stays connected the entire time, so that you end up with just one town to destroy at the end. I think playing the game helps build the intuition needed to see this.

This is based on John Conway's proof in The Symmetries of Things.

I've always thought this was a nicely explained and illustrated proof. Conway does a lot of proofs like this (see Winning Ways). He'll give super memorable mnemonics for the different objects involved in the proof and will invent stories to give "motivation" to various players who are trying to achieve certain goals in the invented world. The strategy allows us to leverage our "social strategic" mind to understand the proof.

It's also a form of "playing algorithm" which is a familiar strategy to us (Glen's Bubble Sort, Papert's "playing turtle", etc.)

Some things I learned while making this:

- Working with clay suggested things not possible on the flat page. I thought I would need to have some sort of video animation to show the unfolding. The 3D figures let you do a 3D animation where you can physically handle each one of the "frames".

- I did the programming using an "object model" similar to what Bret has proposed. The object types are Faces, Vertices, Edges, and Pirates (the game works with multiple Pirates). The Faces, Vertices, and Edges have render methods to illuminate the table. The "state" properties (is it pillaged or not) and location properties are observables. There are also some "derived" observables, for example is a Face, Edge, or Vertex "threatened" (in which case it turns red).

The main difference from doing it the traditional object oriented way is that I had a global "world" that had references to all of my objects and instead of traversing references from object to object I would instead do "queries" on the world (for example computing the "threatened" observable by querying all of the Pirates' locations).

I imagine this could be a whole "station" in our gallery (in the "exploratorium" section). I would like if there were a couple of example polyhedra (not just a cube) that you could put on the table and then you could play the game on those maps. Maybe you could draw your own maps too, or have them randomly generated. The game wants sound effects too.

There are limitations to having everything exist in one "screen". I would like the Faces, Edges, Vertices counters to be somewhere else, not exactly flat on the table.

I'm going to put this away for now to work on the Protrackers, which will make developing this game (and other things like it) easier.