On the other hand, 7±2 says that things, once really understood, need to be used as "things" -- so this is the "understanding"-cum-"performance" double learning activity. Marvin used to say that "The trouble with New Math is you have to understand it every time you use it!" (and this is too much).
One of my favorite articulations of this is John Mason's paper "When is a Symbol Symbolic?"
He reinterprets Bruner's enactive-iconic-symbolic not as inherent properties of a representation, but a person's relationship to the representation

and describes a kind of spiral where "symbols" eventually become "enactive" so they can be used as components in some larger symbolic expression.

A couple of more complex examples that I like to think about are, say, a wave equation and a low-pass filter:
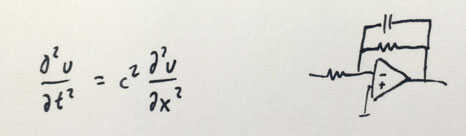
You need to be able to recognize and think about these things as "things" with a higher-level meaning; you need to be able to see a wave or a filter, not just a collection of low-level parts. At the same time, the representation is not a black box -- while thinking about the filter as a filter, you simultaneously see the opamp and the capacitor etc, and "feel" the roles that these components play.
(This is like looking at word in an alphabetic language; you recognize it as a meaningful word while simultaneously seeing individual letters and understanding their roles, which allows you to vary words or invent new ones.)
When looking at a more complex circuit, say, the implementation of an op-amp:
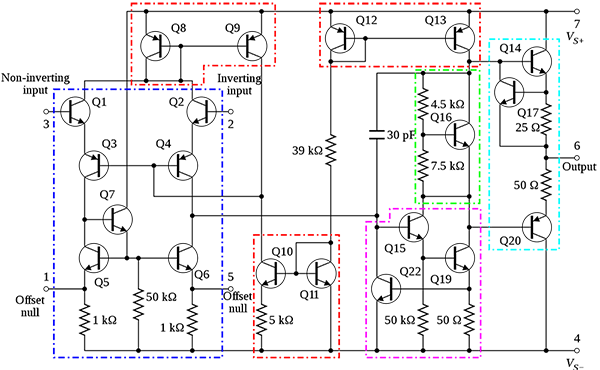
an experienced person's eye will automatically carve out "words" -- high-level meaningful blocks -- these components act as a differential pair, these act as a current mirror, etc. (I guess whoever drew the picture above already did that for you with colored boxes!)
Once you've recognized these things, you can run on your prior understanding -- you already know how current mirrors work, you don't have to derive that from scratch every time, you just recognize them as old friends and trust them. (They are the red boxes above.) At the same time, again, they are not black-boxed, so if some assumptions are being violated, that can jump out at you too -- "wait, I don't think this mirror is going to work, it's not being biased properly".
I think that it also may provide a path to learning in that, as a beginner, you can copy a current mirror out of a book and use it as a "macro" without fully understanding it, but as time goes on and you become more fluent, you start to see "into" it and understand what it "means". (Especially as you run into situations where you need a variation on it, or where it fails because assumptions don't hold.) I see this as the same process that Mason described with 1,2,3 going from symbolic to enactive.
This sort of simultaneous-part-and-whole doesn't show up as much in software, I think, because in our current languages, the components are so weak. The wave equation can describe such rich behavior in such a compact form because the language of partial differential equations describes a relationship between things instead of a procedure. (Likewise with electronics; you can think of electronic components just as terms in an ODE.) In both PDEs and electronics, a small number of components can pack a big punch. So you can have a compact representation where you recognize both the high-level punch and the low-level components simultaneously.
In most programming languages, you need a huge pile of terms in order to do anything interesting, so it's hard to see a meaningful "whole". So you sweep the pile into a procedure definition, which you can invoke with one line, and now you can't see the "parts".
On Mar 1, 2016, at 4:15 AM, 'Alan Kay' via ALL wrote:I agree that it is partly 7±2 problems, but it is also a deeper problem of the conflict between our brains wanting (and being able to deal with gestalts much more readily than "parts and wholes"). We are more primate like than we wish to believe! So, one of things that goes on is that things that really do have parts are treated as wholes, and as "whole words" and "whole utterances" (Joe Becker's phrasal lexicon).Note that the last inventions made in writing (instead of the first) were to write down component sounds, and the very last was to notice that vowels were component sounds too (this was a roughly 3000 year journey, and why the kids are having problems is right in the problems of inventing writing in the first place). The kids are treating the line of code as a "word" rather than a construction. (And the terrible use of "=" is not helping one bit, because this is one of a number of operators that should not be overloaded with a meaning that is not close enough to the other meaning it has -- this is just bad and should not be used in programming languages regardless of stupid traditions ...).When the Japanese got 2nd graders to do animations in Etoys, the kids treated the two liner Etoys program as "a macro" that did what it did. We put this in as a program for children to write (in 4th grade and later, not for 2nd grade) instead of an animation feature to help with this problem of monolithic magic features. Another one was to have children program their one "ramps" of increasing or decreasing a variable each tick. I don't recall that we tested how monolithic this became for them. But there was no question that they were not confused by the variable part of this.My personal take on the math part of all this is that it is probably not doing a learner a favor to use something without understanding in order to do something else. (Math is one of the few human inventions that can be completely understood, and a lot of its flexible power comes from practitioners being able to understand). On the other hand, 7±2 says that things, once really understood, need to be used as "things" -- so this is the "understanding"-cum-"performance" double learning activity. Marvin used to say that "The trouble with New Math is you have to understand it every time you use it!" (and this is too much).CheersAlan
From: "Guzdial, Mark"
To: John Maloney
Cc: Cathleen Galas ; Communications Design Group
Sent: Monday, February 29, 2016 4:37 PM
Subject: Re: [cdg] computational thinking, school math, NY Times article
Hi John,
I agree with your analysis. I had the same What?!? reaction, then realized that it's just understanding coming in pieces. They're not willing to question "x = getX(pixel)" while they focus on the new parts.
I have a blog post I'm working on (scheduled to come out two weeks from today) on characterizing student understanding of notional machines, based on a recent Dagstuhl Seminar I went to. I'll share that with the group when it's ready.
- Mark
________________________________________
From: John Maloney <****************>
Sent: Monday, February 29, 2016 3:58 PM
To: Guzdial, Mark
Cc: Cathleen Galas; Communications Design Group
Subject: Re: [cdg] computational thinking, school math, NY Times article
Hi, Mark.
Thanks for this story. It's an interesting insight into the thought process of beginning programmers.
My first reaction was to be horrified at the "superstitious thinking" of those students.
Then I started thinking about total beginner situations that I've been in -- such as learning to make reeds for my dulcian. There are dozens of parameters that determine whether a reed will work well. It's a huge design space, and when you've made only a few dozen reeds you've only scratched the surface. Thus, when you do manage to make a reed that works well, you try to reproduce that success by doing everything in the exactly same way and keeping all the parameters the same, even though you're fully aware that some of the parameters don't matter. One reason for my resistance to exploring is that making a reed as non-expert is an investment of several hours of work, and you don't find out until close to the end of that time if the reed is going to work. Failed experiments are costly.
I think the psychology of a beginning programmer is similar to that of a beginning reed maker. They've learned some building blocks that work for them. When tackling a new problem, such as the Japanese flag problem, they'd rather focus their attention on the new aspect of that problem. Not being entirely sure which things do and don't matter about "x = getX(pixel)" -- and perhaps having had experiences where a small syntax error or typo lead to hours of frustration -- they take a conservative approach and use this building block verbatim.
As a beginner grows in experience, they start to discover which things do and do not matter. With increasing confidence in their ability to solve problems, they start to take chances, to experiment with parameters, and learn alternate ways to accomplish the same task. As Neils Bohr wrote, "An expert is a man who has made all the mistakes which can be made in a very narrow field." The process of becoming an expert simply takes time. Our job as educators and builders of systems for beginners is to help beginners make "mistakes", gather experience, and build their confidence more quickly.
Blocks languages like Scratch may speed up this process, in part by removing a whole class of frustrating typographical and syntax errors that can be extremely costly for beginners, and in part by supporting rapid and low-cost experimentation. Scratch beginners are just as likely as any beginner to cling to techniques or code fragments without fully them, but I haven't seen Scratch beginners manifest the particular phenomenon you've described: bonding to particular variable names. If you get a chance to teach your media computation course using GP, I'll be curious to know what differences you see.
-- John
On Feb 29, 2016, at 2:56 PM, Guzdial, Mark <****************> wrote:
> Thanks for sharing these, Kat!
>
> I had an experience with my students this morning that connects to this question. I wholly believe that we can use computational environments to encourage development of numeracy. I've been thinking about how we get students to think at the meaning-level and not just the notation-level.
>
> After lecture (big -- 164 students) on Monday mornings, I go work an hour at our course "helpdesk" where students come up with their homework questions. That gives me chance to work with students 1:1 (or close).
>
> My students are currently working on a problem where they're trying to take an input picture and make it look like a Japanese flag: Make the background more white, and put a red circle in the middle:
> <pastedImage.png>
>
> Students are having trouble drawing the red circle in the middle. The assignment recommends taking a brute force approach: consider each pixel in the picture, and if it's within a radius from the middle, make that pixel red. The assignment gives the students the formula for distance between two points:
>
> <pastedImage.png>
>
> I was working with two students who both came in struggling with this same problem. I got them to define the center point (in Python):
>
> x1 = getWidth(picture) / 2
> y1 = getHeight(picture) / 2
>
> No problem. They were with me that far. They knew how to write a loop for all pixels:
> for pixel in getPixels(picture):
>
> No problem. Then I told them to get the coordinates of the given pixel. They each wrote:
> x = getX(pixel)
> y = getY(pixel)
>
> I said, "I want to make it obvious to you how to use the distance formula, so why don't you call those variables x2 and y2."
>
> Both students stopped and just stared at me. One said, "But, x is getX(pixel)!"
> "Sure, but that 'x' is just a variable name. Let's call it x2."
>
> They just looked at each other, thanked me for my time, and went off to work together at another part of the lab. They had seen the line "x = getX(pixel)" so often that they treated it like a magic spell. It could only work if you said it exactly right. I looked in on them later, and they *did* eventually get it. But they used x and y, not x2 and y2.
>
> I was surprised at their hesitancy. They understood how assignment worked in other contexts, e.g., they had no problem setting x1 and y1. But they put their trust in the notation and in details (like variable names) that don't really matter. They did figure out in the end -- they were successful at making the Japanese flag effect using the distance formula.
>
> These students are developing computational literacy (like the development of numeracy), but it's in pieces, in fits and starts. They rely too much on the surface level features yet.
>
> The story of these students feels similar to me to the NYTimes piece. I'm trying to get them to think flexibly about what they're doing. The students want to memorize formulas and write programs by rote.
>
> - Mark
>
>
> --
> ************************
> To post to this group, send email to ****************." href="mailto:****************." class="">****************.
--
************************
To post to this group, send email to ****************." href="mailto:****************." class="">****************.--
************************
To post to this group, send email to ****************.--
************************
************************